This poster appeared at the 2010 CMS Winter Meeting.  Download the pdf for a larger version.

This page will be updated as new publications appear.

A careful search reveals the following publications and mentions of tatami tilings in mathematics:

Mitsuyoshi Yoshida, Japan 1641, Jinkōki ( translated as “Inalterable Treatise”, first published in 1627 according to britannica.com).

• Knuth reprints a 6 x 5 dimer (1 x 2) tiling from Yoshida’s text in The Art of Computer Programming

David Wolfe, Tom Rodgers, 2002, Puzzlers’ Tribute: A Feast for the Mind.  Puzzle by Yoshiyuki Kotani, Y2K problem of dominoes and tatami carpeting.

• Some of this puzzle can be seen in the Amazon.com preview for the hardcover, page 413.  The puzzle seen in the preview is: Find a shape that has exactly 2000 domino tatami tilings.

Dean Hickerson, 2002: OEIS http://oeis.org/A068920/a068920.txt

• Treats fixed height dimer (1 x 2) tilings and finds recurrences for them.  References to several related OEIS sequences.

• As of October 24, 2011, searching oeis.org for “tatami” returns 34 sequences related to tatami tilings.

Knuth, 2009: The Art of Computer Programming, volume 4, fascicle 1B, Binary decision diagrams, exercise 215 and errata.

• Exercise on dimer (1 x 2) tilings:  “Find all domino coverings of a chessboard that are also tatami tilings”

Frank Ruskey and Jennifer Woodcock, 2009: Counting Fixed-Height Tatami Tilings, Electronic J. of Combinatorics.

• Generating function for fixed height dimer tilings, stemming from Knuth’s exercise, above.

Alhazov, Morita, and Iwamoto, 2009: A note on tatami tilings, Proceedings of 2009 LA Winter Symposium.

• Following Ruskey and Woodcock, this paper treated tilings with exactly one monomer (1 x 1).  It motivates further the study of arbitrary monomers but was written prior to our discovery of their structure.

A mention by Don Knuth at theory lunch, 2010

Alejandro Erickson, Frank Ruskey, Mark Schurch, Jennifer Woodcock, 2010: Auspicious Tatami Mat Arrangements, 16th COCOON Conference, LNCS 6196, pp. 288–297.

• Full characterization of the structure monomer-dimer (1x1 and 1x2) tatami tilings of rectangular regions.
• Maximum number of monomers in an $r x c$ tiling is max(r,c) or max(r,c)+1 and has parity the same as rc.
• The number of $n\times n$ tilings with $n$ monomers is $n2^{n-1}$.
• The generating function for fixed height monomer-dimer tilings is a rational generating function.

Alejandro Erickson, Frank Ruskey, Mark Schurch, Jennifer Woodcock, 2011. Monomer-Dimer Tatami Tilings of Rectangular Regions. Electronic Journal of Combinatorics, 18(1) (2011) P109, 24 pages.

• Expanded journal version of the above

A. Erickson, M. Schurch, 2011: Enumerating tatami mat arrangements of square grids, in 22nd International Workshop on Combinatorial Algorithms, University of Victoria, June 20-22, volume 7056 of Lecture Notes in Computer Science (LNCS), Springer Berlin / Heidelberg, 2011, p. 12 pages.

• Abstract:     We prove that the number of monomer-dimer tilings of an $n\times n$
  square grid, with $m<n$ monomers in which no four tiles meet at any
  point is $m2^m+(m+1)2^{m+1}$, when $m$ and $n$ have the same parity.
  In addition, we present a new proof of the result that there are
  $n2^{n-1}$ such tilings with $n$ monomers, which divides the tilings
  into $n$ classes of size $2^{n-1}$.  The sum of these over all $m\le
  n$ has the closed form $2^{n-1}(3n-4)+2$ and, curiously, this is equal
  to the sum of the squares of all parts in all compositions of $n$.

Tatamibari, Nikoli

• We are given a rectangular grid with certain symbols.  The goal is to find a certain subdivision of the grid into rectangles which satisfies the tatami condition.  My own post about this puzzle is here.

2010 Frank Ruskey, Alejandro Erickson

• Players take turns adding tiles to a rectangular grid.  They must not violate the tatami condition and the first player with no available move loses.

Tomoku! 2010, Martín Matamala, Alejandro Erickson

• The player must reconstruct a tatami tiling given its row and column projections.
• A website, web game and book are dedicated to this at http://tomokupuzzle.com

Tatami dots and boxes, 2010, Alejandro Erickson, Gwen Temmel

• Played just like dots and boxes except that no four lines may touch at any point.

Water striders, Frank Ruskey, Alejandro Erickson, Brian Wyvill

• Players place x shaped pieces which must not overlap.  The first player with no available move loses.  This is inspired by the rays formed by the tatami configurations called bidimers and vortices and the desire to pack them.

There is another puzzle due to Knuth I think, with 1x3 tiles, but I don’t remember where I saw it.

I had a word with Ron Graham at the 2010 CMS Winter Meeting and he mentioned a short paper of his in which he talks about fault-free dimer tilings.  A fault-free tiling of a rectangular grid is one in which every interior grid line intersects at least one tile.  Here is a 6 x 6 tiling with two faults.

Ron Graham gives a clever argument, due to S. W. Golomb and R. I. Jewett, that no 6 x 6 fault-free dimer tiling exists.  Try to prove it yourself! (hint:  a dimer blocks exactly one potential fault.  Use elementary arguments).

Let's ask the obvious question.

For which dimensions r x c can we have fault free tatami-dimer tilings?

The answer is simple.  It never happens, except, in the 1 x 2 rectangle.  I'll allow you to convince yourself (in keeping with the low production value of this post) by looking at this:

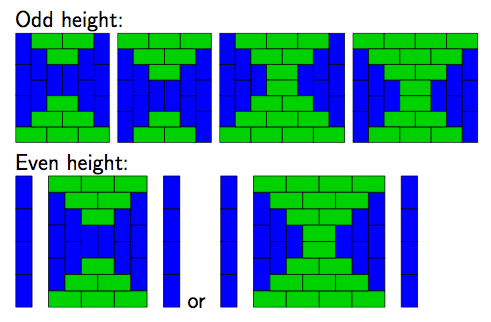
Dimer tatami tilings of rectangles are all compositions of these configurations.  Since their compositions create fault lines, we may assume that a fault-free tiling has a single bidimer (the configuration in the middle).  But each of these clearly has at least one fault line too.

(disclaimer:  I'm posting this before I'm done thinking about it.  If you want to cite it you should contact me and I'll write a better proof)

Tutorial video below!

{swf;http://www.alejandroerickson.com/joomla/tatami/tomoku_game.swf;}

The Emperor needs you to prepare an auspicious floor for his tea ceremony, but the Ikea instructions only give the row and column projections of the tiling!  You must race the clock to reconstruct it before the Emperor has your head!

A tatami mat is a 1x1 or a 2x1 tile, used for traditional Japanese floorings.  In certain applications, it is "unlucky" to have four mats meeting at one point.

The game was conceived during a conversation with Martín Matamala , a mathematician from Universidad de Chile.  It is related to my PhD thesis work on the Tatami condition.  More details will be published in the upcoming journal version of "Auspicious tatami arrangements" by Frank Ruskey, Mark Schurch, Jennifer Woodock and myself.  A preprint should appear soon at http://arxiv.org/.

The in-game music is by Safary on ccmixter.org and the background photo is by 663highland on Wikipedia.

Here is an instructional video with wicked awesome Whaledub music from .  The music can be found at soundcloud.com - search for sness.

I appreciate your input and feedback in the comments.  Please link to the game through my site so I can measure the traffic before working on a commercial version.  If you are interested in doing the artwork for the commercial version, please contact me at alejandro.erickson@gmail.com