I had a word with Ron Graham at the 2010 CMS Winter Meeting and he mentioned a short paper of his in which he talks about fault-free dimer tilings.  A fault-free tiling of a rectangular grid is one in which every interior grid line intersects at least one tile.  Here is a 6 x 6 tiling with two faults.

Ron Graham gives a clever argument, due to S. W. Golomb and R. I. Jewett, that no 6 x 6 fault-free dimer tiling exists.  Try to prove it yourself! (hint:  a dimer blocks exactly one potential fault.  Use elementary arguments).

Let's ask the obvious question.

For which dimensions r x c can we have fault free tatami-dimer tilings?

The answer is simple.  It never happens, except, in the 1 x 2 rectangle.  I'll allow you to convince yourself (in keeping with the low production value of this post) by looking at this:

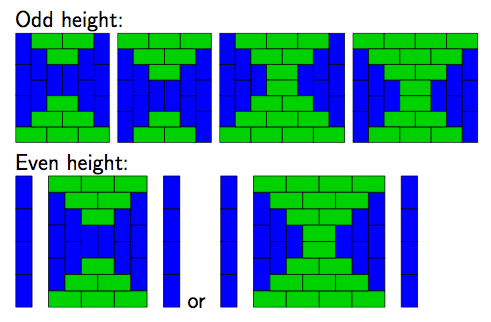
Dimer tatami tilings of rectangles are all compositions of these configurations.  Since their compositions create fault lines, we may assume that a fault-free tiling has a single bidimer (the configuration in the middle).  But each of these clearly has at least one fault line too.

(disclaimer:  I'm posting this before I'm done thinking about it.  If you want to cite it you should contact me and I'll write a better proof)