My tatami work at Moka House was briefly interrupted by a very enjoyable coffee with my friend Gwen Temmel today, during which she suggested that tatami tilings looked a little like the game Dots and Boxes.  A light went on inside me and I said,

LET’S PLAY DOTS AND BOXES WITH THE TATAMI CONDITION,

which just about as much inward enthusiasm.  The result was this:

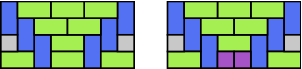
If it is not obvious already, the game is played just as Dots and Boxes, but you may not create a four-valent site.   In other words, no pluses may be created.  If a player makes a box they must go again, no player may pass, the game ends when no legal move exists.

Playing this game is more fun, in my opinion than the original Dots and Boxes, and there is a mathematical curiosity that comes up.  Dots and Boxes ends when all bonds (edges) have been added, whereas this one has many different endings, each of them a maximal bond animal of a (typically) rectangular integer grid.  How many of these are there?

Notice that some tatami tilings are not maximal in this sense.  When a bidimer (formerly hamburger) has a long edge on the boundary of the grid, one of its dimers can be split into monomers.  I think this is the only such case, however.

Have you played Tatami Dots and Boxes?  Tell me about it in the comments!